Introduction
With the proliferation of digital phased arrays in commercial and aerospace and defence applications, there are many engineersworking on various aspects of the design who have limited phased array antenna familiarity. Phased array antenna design is not new, as the theory has been well developed over decades; however, most of the literature is intended for antenna engineers well versed in the electromagnetic mathematics. As phased arrays begin to include more mixed-signal and digital content, there are many engineers who could benefit from a much more intuitive explanation of phased array antenna patterns. As it turns out, there are many analogies between the behaviour of phased array antennas and the discrete time sampled systems that the mixed-signal and digital engineers work with every day.
These articles are not intended to create antenna design engineers, but rather to help the engineer working on a subsystem or component used in a phased array to visualise how their effort may impact a phased array antenna pattern.
Beam Direction
First, let’s look at an intuitive example of steering a phased array beam. Figure 1 provides a simple illustration of a wavefront striking four antenna elements from two different directions. A time delay is applied in the receive path after each antenna element, and then all four signals are summed together. In Figure 1a, that time delay matches the time difference of the wavefront striking each element. And in this case, that applied delay causes the four signals to arrive in phase at the point of combination. This coherent combining results in a larger signal at the output of the combiner. In Figure 1b, that same delay is applied; however, in this case, the wavefront is perpendicular to the antenna elements. That applied delay now misaligns the phase of the four signals, and the output of the combiner is significantly reduced.

In a phased array, time delay is the quantifiable delta needed for beam steering. But time delay can also be emulated with a phase shift, which is common and practical in many implementations. We will discuss the impact of time delay vs. phase shift in the section on beam squint, but for now let’s look at a phase shift implementation, and then derive the calculation for beam steering with that phase shift.
Figure 2 shows this phased array arrangement using phase shifters rather than time delay. Note that we define the boresight direction (θ = 0°) as perpendicular to the face of the antenna. A positive angle θ is defined to the right of boresight, and a negative angle is defined to the left of boresight.
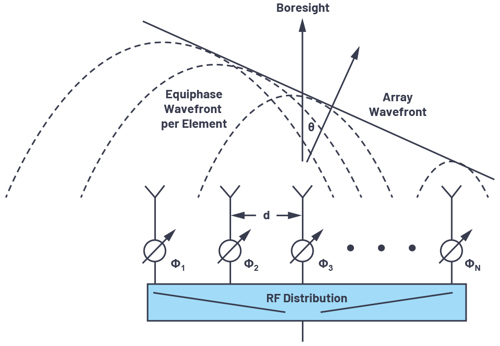
To visualise the phase shift needed for beam steering, a set of right triangles can be drawn between adjacent elements, as shownin Figure 3. Where ΔΦ is the phase shift between those adjacent elements.
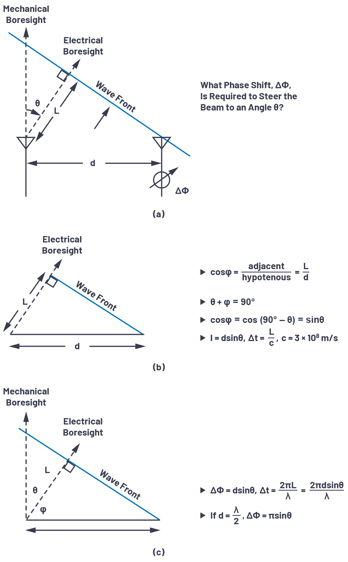
Figure 3a defines the trigonometry between those elements, with each element separated by a distance (d). The beam is pointedin a direction off boresight, θ, which is an angle, φ, from the horizon. In Figure 3b, we see that the sum of θ + φ = 90°. This allows us to compute L, the delta distance of wave propagation, as L = dsin(θ). The time delay to steer our beam is equal to the time it will take for the wavefront to traverse that distance, L. If we think of L as a fraction of the wavelength, then a phase delay could besubstituted in for that time delay. The equations for ΔΦ can then be defined relative to θ, as shown in Figure 3c and repeated in Equation 1.

If the spacing between elements is exactly one half of the signal wavelength, then this can further be simplified to:

Let’s work out an example with these equations. Consider two antenna elements spaced 15mm apart. If a 10.6GHz wavefront is arriving at 30º from mechanical boresight, then what is the optimal phase shift between the two elements?
So, if our wavefront is arriving at θ = 30º, then if we shift the phase of the neighbouring element by 95º, we will cause the individual signals of both elements to add coherently. This will maximise the antenna gain in that direction.
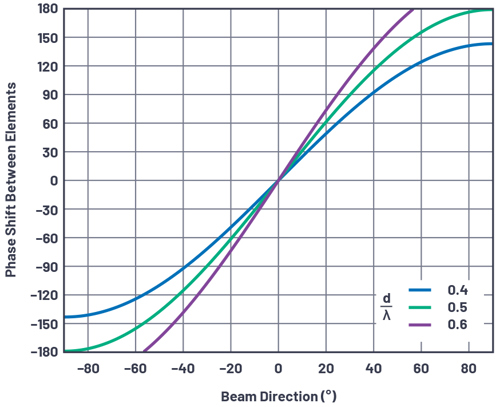
For a better appreciation of how the phase shift varies with the beam direction (θ), these equations are plotted for a variety of conditions in Figure 4. Some interesting observations can be made from these graphs. For the case of d = λ/2, there is an approximate 3 to 1 slope near boresight, which is the π multiplier in Equation 2. This case also shows a full 180° shift betweenelements provides a theoretical 90° shift in beam direction. In practice, with real element patterns, this is not realisable, yet the equations do show the theoretical ideal. Note that for d > λ/2, no amount of phase shift provides a full beam shift. Later, we will see this case can lead to grating lobes in the antenna pattern, and this graph provides a first indicator that something is different withthe d > λ/2 case.
A Uniformly Spaced Linear Array
The equations developed above have applied to just two elements. Yet a real phased array can be thousands of elements spaced across two dimensions. But for our purposes here, let’s just consider one dimension: a linear array.
A linear array is a single element wide with N number of elements across. The spacing may vary, but often it is uniform. Therefore, in this paper, we will set the spacing between each element to a uniform distance, d, (Figure 5). Although simplified, this uniformly spaced linear array model provides the foundation for insight into how the antenna pattern is formed vs. a variety of conditions. We can further apply the principles of the linear array to understand two-dimensional arrays.

Near Field vs. Far Field
So how can we take the equations previously developed for an N = 2 linear array and apply them to an N = 10,000 linear array? Right now, it seems that each antenna element has a slightly different angle pointing to the spherical wavefront, shown in Figure 6.
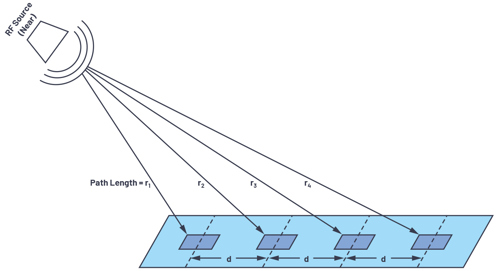
With the RF source near, the incident angle varies for each element. This situation is called the near field. We can work out allthese angles, and sometimes we need to do this for antenna testing and calibration as our test setup can only be so large. But, if we instead just assumed that the RF source was far away, then we’d have the case in Figure 7.
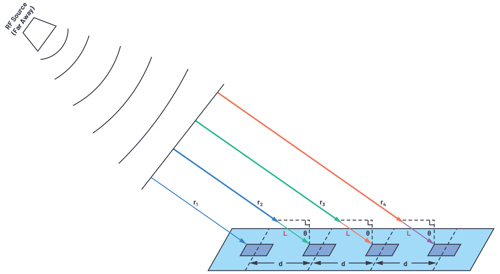
With the RF source far away, the large radius of the spherical wavefront results in wave propagation paths that are approximately parallel. Therefore, all our beam angles are equal, and each adjacent element has a path length that is L = d × sinθ longer than its neighbour. This simplifies the math and means that the two element equations we derived can be applied to thousands of elements, provided they have uniform spacing.
But when can we make the far field assumption? How far is far? It’s a little subjective, but in general, far field is considered anything greater than:

where D is the diameter of the antenna ((N-1) × d for our uniform linear array)
For a small array (small D) or a low frequency (large λ), the far field distance is small. But for a large array (or high frequency), the far field distance could be many kilometres! That makes it hard to test and calibrate the array. For those conditions, a more detailednear model may be used, and then bridge this back to the far field, real-world use of the array.
Antenna Gain, Directivity, and Aperture
Before we go too far, it is helpful to define antenna gain, directivity, and aperture. Let’s start with a clarification on gain vs. directivity, as the two are often interchanged. Antenna gain and directivity are in comparison to an isotropic antenna - which is an ideal antenna that radiates evenly in all directions. Directivity is a comparison of the maximum power measured, Pmax, in a particulardirection to the average power radiated across all directions, Pav. When no direction is defined, directivity is determined by Equation4.

Directivity is a useful metric when comparing antennas as it defines the ability to focus radiated energy. Gain has the same patternof directivity, but gain includes the antenna losses.
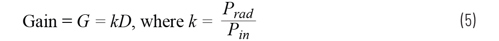
Prad is the total power radiated, Pin is the input power to the antenna, and k accounts for losses in the antenna radiation process.
Next, let’s consider an antenna pattern as a function of a three-dimensional direction and directivity as a function of beamwidth.
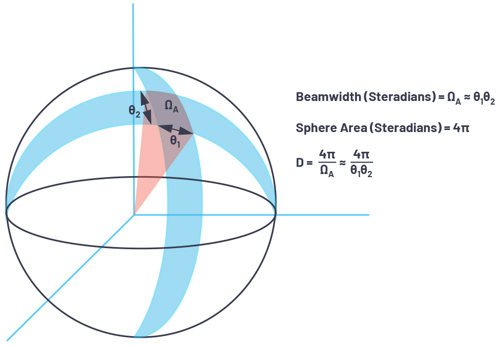
The total surface area of a sphere is 4π2, and an area on a sphere is defined in units of steradians with 4π steradians in a sphere.Therefore, the power density from an isotropic radiator is:

and has units of (W/m2).
There are two angular directions for an area of a sphere. In radar systems, these are commonly referred to as azimuth and elevation. Beamwidths can be described as a function of each angular direction as θ1 and θ2: the combination creates an area on the sphere of ΩA.
Ω is the beamwidth in steradians and can be approximated as ΩA ≈ θ1 × θ2.
Recognising ΩA as an area on the sphere, directivity can then be expressed as:

The third antenna term we’ll consider is aperture. Antenna aperture represents an effective area for receiving electromagnetic waves and includes a function relative to wavelength. The aperture of an isotropic antenna is:

Gain is relative to isotropic radiation, making the effective aperture of an antenna:

Pulling these three terms together, we can see that gain can be considered a function of angle that defines a radiation pattern and accounts for efficiency (or losses) in the antenna.
Array Factor for a Linear Array
At this point, we’re able to predict the optimal time (or phase) delta between elements to achieve maximum antenna directivity. But we’d really like to understand and manipulate the complete antenna gain pattern. There are two main parts to this. First, there is the gain of each individual element of our array (perhaps one patch), called the element factor (GE). Secondly, there is the impact that we can exert through beamforming the array, called the array factor (GA). The full array antenna gain pattern is the combination of the two factors, as shown in Equation 10.

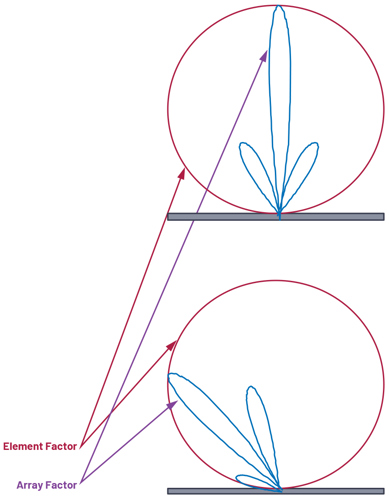
The element factor, GE, is the radiating pattern of a single element in the array. This is defined by the geometry and construction of the antenna, and not something that is varied in operation. It is important to know, as it will limit the gain of our total array - particularly near the horizon. But since we can’t control it electrically, we’ll leave it as a fixed influencer to our total phased array gain equation. For this article, we’ll assume that all the individual elements have the same element factor.
The focus then is on the array factor, GA. The array factor is calculated based on array geometry (d for our uniform linear array) andbeam weights (amplitude and phase). Deriving the array factor for a uniform linear array is straightforward, but the details are best covered in the references cited at the end of this article.
There are some variations in equations used across literature depending on how parameters were defined in the linear array. We use the equations from this article, which results in consistency with our definitions in Figure 2 and Figure 3. Since our primary concern is how the gain changes, it is often more instructive to plot the normalised array factor relative to unity gain. That normalised array factor can be written as Equation 11.

We have already defined beam angle θ0 as a function of phase shift between elements ΔΦ; therefore, we can also write the normalised antenna factor as Equation 12.
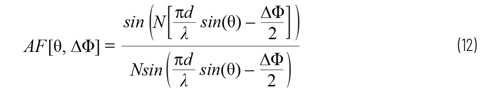
The conditions assumed in the array factor equation include:
Next, using these equations, we plot the array factor for several array sizes.
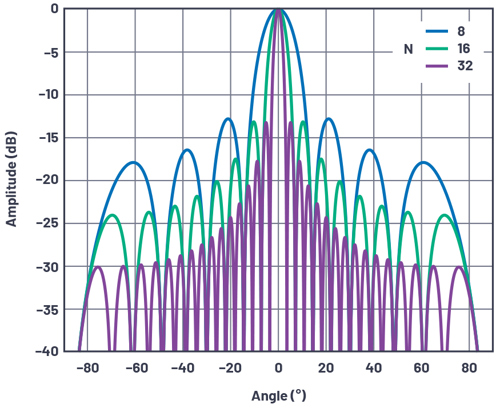
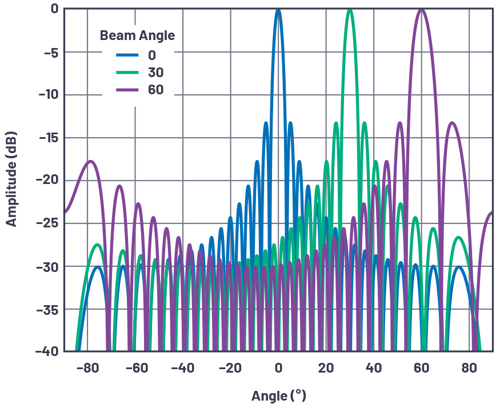
Some observations from these figures include:
Beamwidth
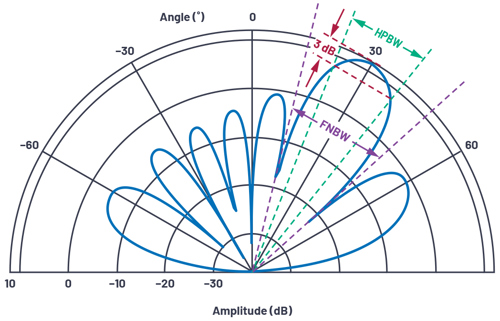
Beamwidth provides a metric of angular resolution for antennas. Most commonly, beamwidth is defined by either the half-powerbeamwidth (HPBW) or the null-to-null spacing of the main lobe (FNBW). To find the HPBW, we move 3dB down from the peak and measure the angular distance, as shown in Figure 12.
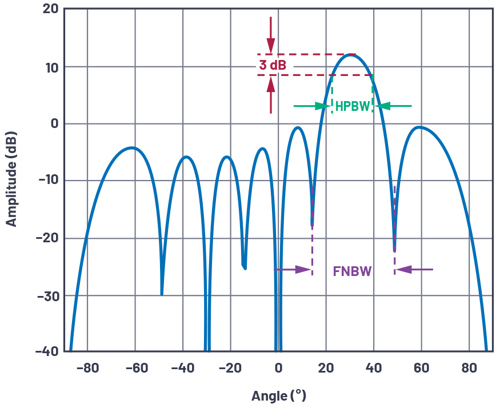
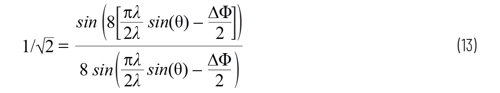
Then solving for ∆Φ gives 0.35rad. Use Equation 1, and solve for θ:
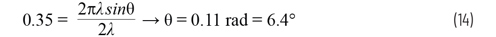
That θ is the peak to 3dB point, which is half of our HPBW. Therefore, we simply double it to arrive at the angular distance between the 3dB points. This results in an HPBW of 12.8º.
We could repeat this for an array factor equal to 0 and obtain the first null-to-null spacing angle of FNBW = 28.5º, for the previously mentioned conditions.
For uniform linear arrays, an approximation for HPBW [1,2] is given as Equation 15.


From this graph, it is worth noting some observations relative to array sizes under development in the industry.
Combining Element and Array Factors
The previous section only considered the array factor. But to find the total antenna gain, we also require the element factor. Figure 14 illustrates an example. In this example, we use a simple cosine shape as the element factor, or normalised element gain, GE(θ). The cosine rolloff is common in phased array analysis and can be visualised if considering a flat surface. At broadside, there is a maximum area. As the angle moves away from broadside, the area visible reduces following a cosine function.
The array factor, GA(θ), was used for a 16-element linear array, with a λ/2 spacing, and a uniform radiation pattern. The total patternis a linear multiplication of the element factor and array factor, so in a dB scale, they can be added together.

A few observations as the beam moves off boresight:
Antenna Plots: Cartesian vs. Polar
The antenna pattern plots used so far have been in cartesian coordinates. But it is common to plot antenna patterns in polar coordinates as they are more representative of energy radiating spatially outwards from the antenna. Figure 15 is a redrawn version of Figure 12, but using polar coordinates. Note that this is the exact same data, point for point - it’s just redrawn with a polarcoordinate system. It is worthwhile to be able to visualise the antenna pattern in either representation as both are used in literature. For most of this text, we will use cartesian coordinates as in this representation it can be easier to compare beamwidth and sidelobe performance.
Array Reciprocity
Up until this point, all the diagrams and text have described a signal that the array is receiving. But how would this change for atransmit array? Fortunately, most antenna arrays are reciprocal. Therefore all of the diagrams, equations, and terminology are the same for transmit as they are for receive. Sometimes it is easier to think of the beam as being received by the array. Andsometimes, perhaps in the case of grating lobes, you may find it more intuitive to think of the array as transmitting a beam. In thisarticle, we generally describe the array as receiving a signal. But if this is harder to visualise for you, then you can equally think of the same concepts on the transmit side.
Summary
This concludes Part 1 of this 3-part series. The concept of beam steering with a phased array was introduced. The equations to calculate phase shift across the array for beam steering were derived and shown graphically. Then array factor and element factor were defined with observations of how the number of elements, the spacing between elements, and the beam angle impacts the antenna response. Finally, a comparison of antenna patterns in cartesian vs. polar coordinates was shown.
Upcoming articles in this series will further explore phased array antenna patterns and impairments. We’ll study how antennatapering reduces sidelobes, how grating lobes are formed, and the impact of phase shift vs. time delay in wideband systems. The series will finish with an analysis of the finite resolution of the delay block and how it can create quantisation sidelobes and degradebeam resolution.
Analog Devices: www.analog.com
References
Balanis, Constantine A. Antenna Theory: Analysis and Design. Third edition, Wiley, 2005.
Mailloux, Robert J. Phased Array Antenna Handbook. Second edition, Artech House, 2005.
O’Donnell, Robert M. “Radar Systems Engineering: Introduction.” IEEE, June 2012. Skolnik, Merrill. Radar Handbook. Third edition, McGraw-Hill, 2008.
About the Author
Peter Delos is a technical lead in the Aerospace and Defense Group at Analog Devices in Greensboro, NC. He received his B.S.E.E. from Virginia Tech in 1990 and M.S.E.E. from NJIT in 2004. Peter has over 25 years of industry experience. Most of his career has been spent designing advanced RF/analogue systems at the architecture level, PWB level, and IC level. He is currently focused on miniaturising high performance receiver, waveform generator, and synthesiser designs for phased array applications. He can be reached at peter.delos@analog.com.
About the Author
Bob Broughton started at Analog Devices in 1993 and has held positions as a product engineer and an IC design engineer, and is currently the director of engineering in the Aerospace and Defense Business Unit. Prior to ADI, Bob worked at Raytheon as an RF design engineer and at Peregrine Semiconductor as an RFIC designer. Bob graduated with a B.S.E.E. from West Virginia University in 1984. He can be reached at bob.broughton@analog.com.
About the Author
Jon Kraft is a senior staff FAE in Colorado and has been with ADI for 13 years. His focus is software-defined radio and aerospace phased array radar. He received his B.S.E.E. from Rose-Hulman and his M.S.E.E. from Arizona State University. He has nine patents issued, six with ADI, and one currently pending. He can be reached at jon.kraft@analog.com.










Water Sector Talent Exodus Could Cripple The Sector
Maybe if things are essential for the running of a country and we want to pay a fair price we should be running these utilities on a not for profit...